Red Black Tree

  • 이진탐색트리

    • 이진탐색트리 중에 한쪽에만 노드들이 치우쳐져 균형잡힌 트리가 만들어지지 않을 수 있다. → 이럴 경우 탐색을 위한 시간이 증가하게 된다.

      → 이를 보완하여 균형잡힌 트리를 만들고자 만들어진 자료구조가 Red Black Tree

  • Balanced Binary Search Tree (균형잡힌 이진트리)
    • 높이는 무조건 logn ⇒ 시간복잡도 : O(logn)
  • 각 노드의 색깔을 Red, Black 중에 선택하여 주어진 조건을 만족시켰을 때 성립하는 Tree

Red Black Tree의 조건

1️⃣ 모든 노드의 색깔은 Red or Black이다.

2️⃣ 루트노드는 언제나 Black이다.

3️⃣ 모든 Leaf node는 Black이다. (=모든 External node)(NIL)

4️⃣ 노드가 Red라면, 그 노드의 자식노드는 언제나 Black이다. = Red 노드가 연속으로 올 수 없다. (No Double Red)

5️⃣ 모든 Leaf 노드에서 Black Depth는 같다. = 루트에서 말단노드까지의 Black노드의 개수는 언제나 동일하다.

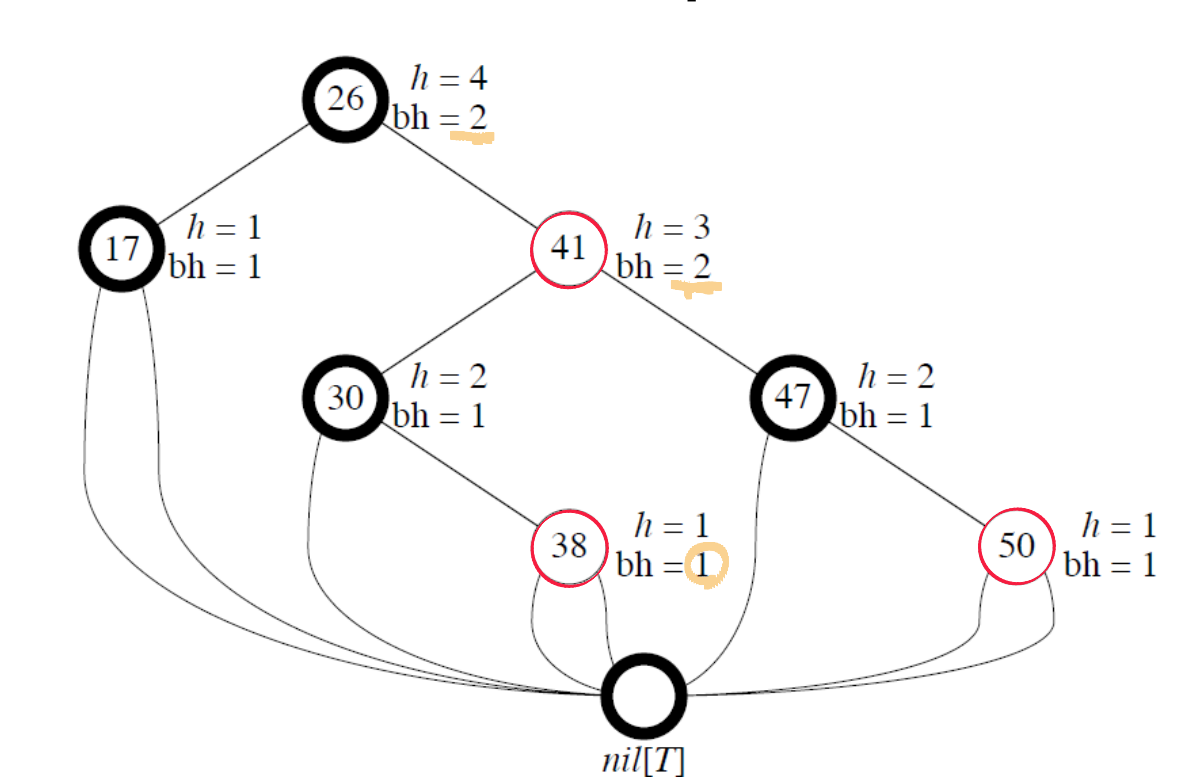
h = height, bh = black height

h = height, bh = black height

  • Height of Node : the number of edges in a longest path to a leaf

  • Black Height of a node : number of black nodes (including nil[T ]) on the path from x to leaf, not counting x.

  • 삽입할 노드는 무조건 Red!!

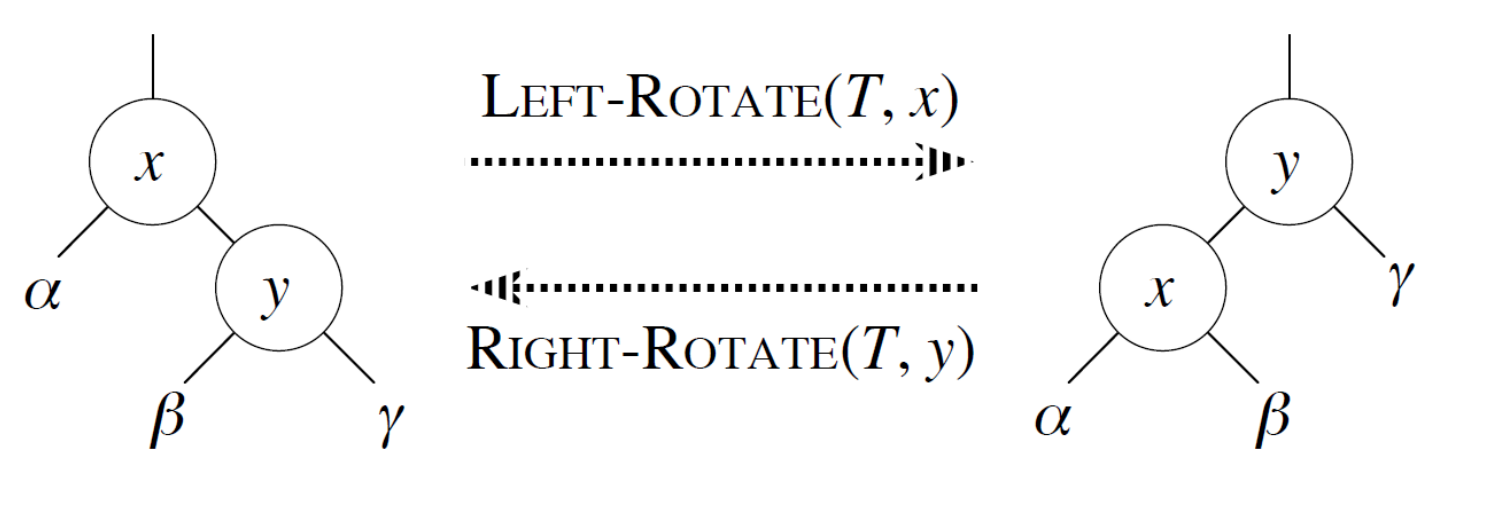
Left and Right Rotation

  • 이진탐색트리의 특성을 유지하면서 왼쪽 혹은 오른쪽으로 회전하는 방법
  • 레드블랙트리에서는 삽입이나 삭제 후 레드블랙특성을 유지하기 위해 사용된다.

Untitled

Insertion

[1]

삽입하려고 하는 노드의 부모노드가 Black인 경우 → 아무 문제없이 노드 삽입 가능

[2]

삽입하려고 하는 노드의 부모노드가 Red인 경우 → Double Red 문제가 발생한다.

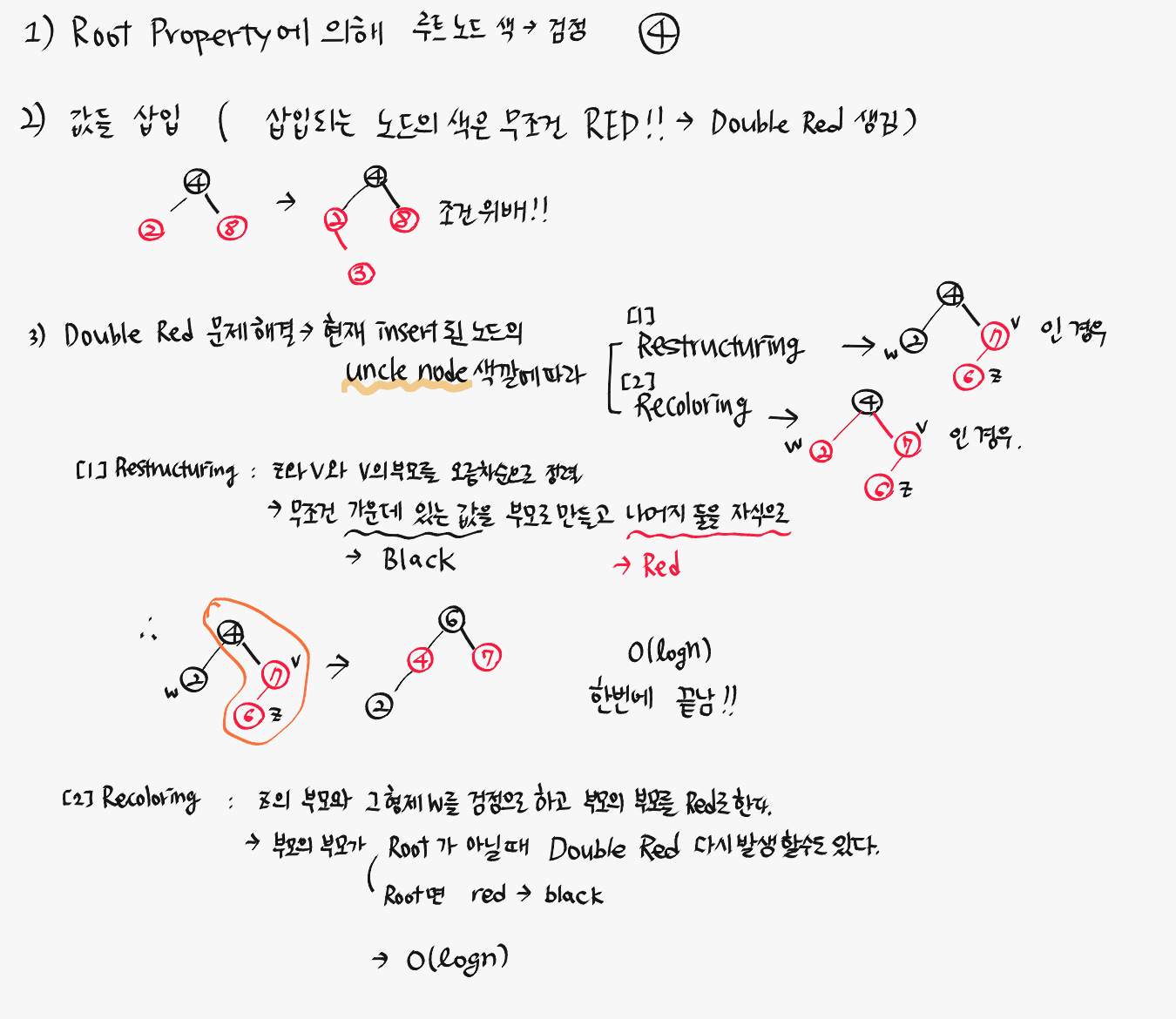
Untitled

+

Restructuring에서 z가 v의 right child일 경우

→ Left Rotation 시킨 후 left child 버전으로 만들어 다시 Restructuring 한다.

Deletion

[1]

삭제하려는 노드(=y)가 Red인 경우 → 그냥 삭제해주면 된다.

[2]

삭제하려는 노드(=y)가 Black인 경우

1) y가 root, x(=y의 child)가 red인 경우 → root가 red가 되는 문제가 발생한다. (2️⃣위반)

2) y의 부모와 x가 모두 red 인 경우 → Double Red 발생 (4️⃣위반)

3) 경로에 y를 포함한 경우 Black node가 한 개 적어진다.(5️⃣위반)

❓How to Fix?? - 노드x에 Extra Black 부여하기

→ 이제 조건5는 성립하지만, 모든 노드는 Red or Black이라는 1번 조건이 위배된다.

  • x 는 doubly black (if color[x] = BLACK) 이거나 red & black (if color[x] = RED)

‼️Idea : extra Black을 트리의 위쪽으로 이동시킨다.

🔻

x가 R&B 면 → 그냥 Black으로 바꿔주면 1)2) 문제 해결

🔻

[Case1] w(=x의 형제) is Red

  • w는 반드시 Black Child를 가지고 있어야 한다.
  • w를 Black으로, x의 부모를 Red로 바꾼다.
  • p[x]를 기준으로 Left Rotate한다.

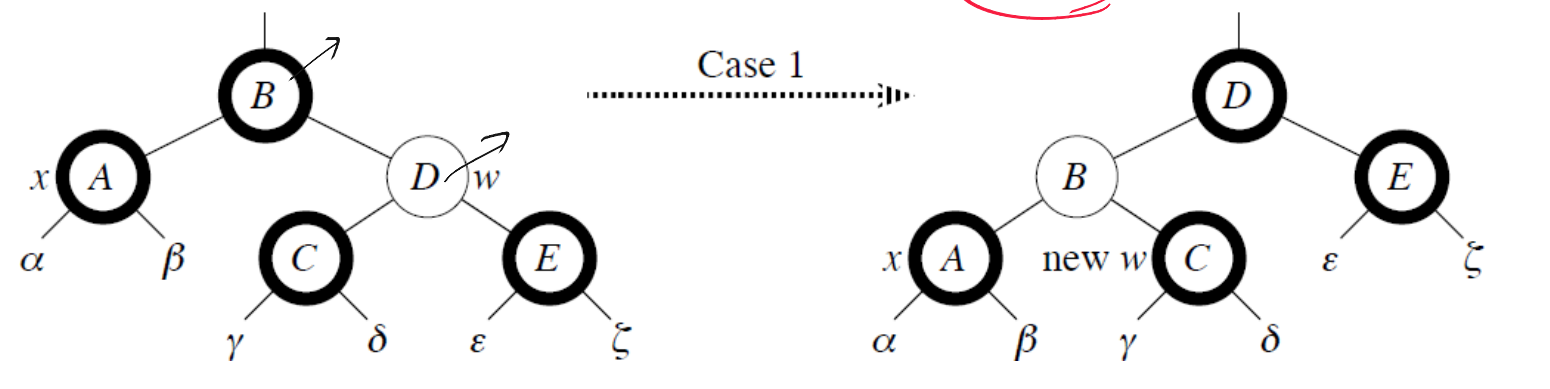
Untitled

  • x의 새로운 형제(=c는) 이전에 w의 자식이었기 때문에 반드시 Black 일것이다.
  • 이 다음 case 2,3,4 를 수행한다.

[Case2] w is Black & w의 자식들 모두 Black

  • x를 singly Black으로, w를 Red로 바꿔준다.
  • x로부터 빼앗은 Black을 p[x]로 전달하고 → p[x]가 이제 new x

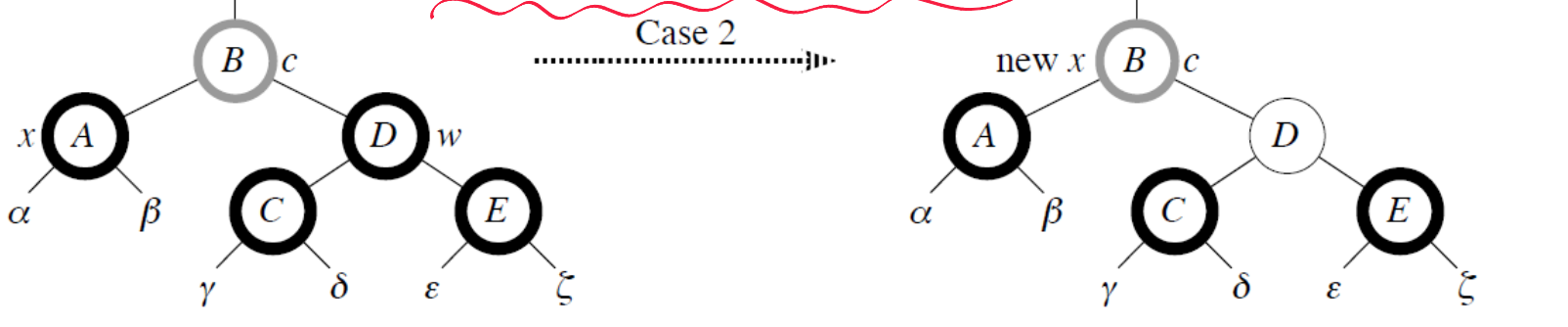
Untitled

⇒

  1. new x (원래 p[x])가 Red 였다면 → new x는 Red&Black → 그냥 Black으로 변환 후 종료한다.

  2. new x가 Black이었다면 → new x는 double Black → loop

[Case3] w is Black & w의 왼쪽 자식이 Red & w의 오른쪽 자식은 Black

  • w를 Red로 바꾸고, w의 왼쪽자식을 Black으로 바꾼다.
  • 그 다음 w에 대해 Right Rotate를 한다.

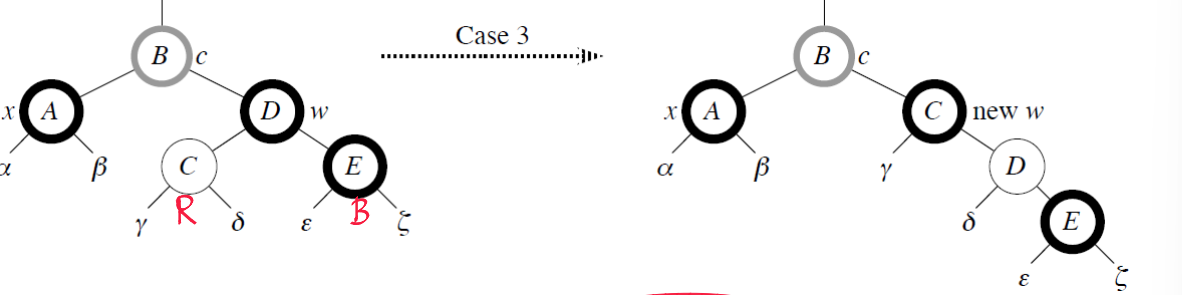
Untitled

  • x의 새로운 형제가 된 new w는 Black이 되고, new w의 오른쪽 자식은 Red가 된다. → Case4로 이동

[Case4] w is Black & w의 왼쪽 자식이 Black & w의 오른쪽 자식은 Red

  • w의 색을 p[x]의 색으로 바꾼다.
  • p[x]의 색을 Black으로, w의 오른쪽 자식을 Black으로 바꾼다.
  • p[x]에 대하여 Left Rotate를 한다.
  • x의 Extra Black을 삭제하여 x를 Singly Black으로 만든다.

예상문제<

  • Red Black Tree란?

    BST를 기반으로하는 트리형식의 자료구조.

    탐색, 입력, 삭제의 시간복잡도가 O(logn)

    BST의 삽입, 삭제, 연산 과정에서 발생할 수 있는 문제점을 해결하기 위해 만들어진 자료구조

  • Red Black Tree의 특징 5가지

  • RBT의 삽입 과정

    1. 삽입된 노드를 red로 지정 : black-height를 최소화하기 위해서

    2. RBT의 특성 위배시, 노드의 색깔을 조정한다

    3. Black-Height가 위배되었을 경우, rotation을 통해 height 조정한다

  • RBT의 삭제 과정

    1. 삭제될 노도의 child의 개수에 따라 rotation방법이 다라진다.

    2-1. 지워진 노드의 색깔이 black이라면 black-height가 1 감소한 경로에 black node가 1개 추가될도록 rotation하고 색깔을 조정한다.

    2-2. 지워진 노드의 색깔일 red라면 violation이 발생하지 않으므로 RBT가 그대로 유지한다.