Single Source Shortest Path Algorithms

💡 단일출발지 최대경로(SSP) : 하나의 출발점에서 각 정점까지 도달하는데 비용을 계산하여 최단경로를 구하는것

🔻

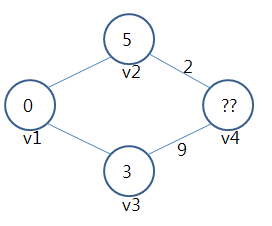
👉v1에서 v4로 가려면 두 가지의 경로가 존재

• v1 -> v2 -> v4
  • v1 -> v2의 비용은 5이고, v2 -> v4의 비용은 2이므로 5 + 2 = 7
• v1 -> v3 -> v4
  • v1 -> v3의 비용은 3이고, v3 -> v4의 비용은 9이므로 3 + 9 = 12

⇒ 두 경로 중 비용이 적은 1번을 선택하는 것이 v1에서 v4의 최단 경로

⇒ 최단 경로는 직전 정점까지의 경로 비용에 영향을 받는다는 것을 알 수 있다.

👉Negative-Weight Edges (음의 가중치)

• 음의 가중치를 허용하여 SSP를 구하는 알고리즘은 Bellman-Ford 알고리즘
• 음의 가중치를 허용하지 않고 SSP를 구하는 알고리즘은 Dijkstra’s 알고리즘

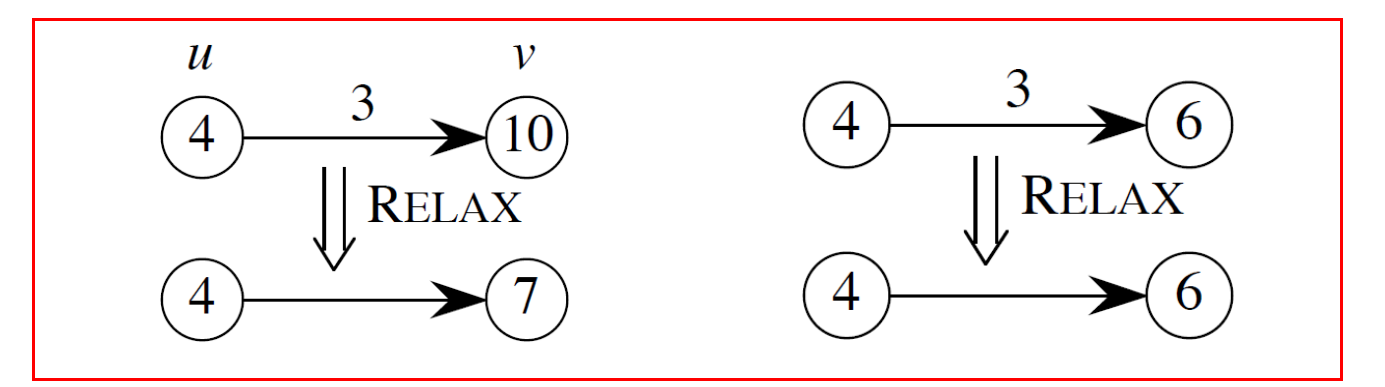
Relaxation

• d[v] 를 정점 v까지의 최단 경로 추정 값, δ(s, v)를 정점 s에서 v까지의 실제 최단경로 비용 이라고 할 때,

Relaxation이란 d[v]값이 δ(s, v)의 상한이 되도록 유지하는 것을 말한다.

• d[v]를 조정하면서 도달해야 할 목적지 = δ(s, v)
• d[v]를 조정하는 함수 : Relax

🔻

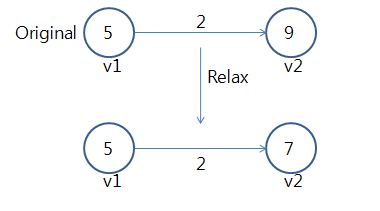
→ Original : d[v2]=9 (SSP를 진행하면서 얻은 최단경로 추정값)

→ 경로를 구하는 방법은 이전 정점( v1 )까지의 경로 비용과 연결된 가중치의 비용을 더하는 것

→ 그래서 d[v1]이 5이고, 연결된 간선의 가중치가 2이므로 d[v2]는 7.

→ 기존에 추정 값 9보다 더 작은 비용이므로 d[v2]를 7로 변경

⇒ 이렇게 비교 연산을 수행하는 것을 Relax 라고 한다.

• Relax란 목적지 정점( v2 )의 추정값과 직전 정점 ( v1 )의 추정값 + 간선의 가중치를 비교해서

목적지 정점의 추정 값을 조정하는 것을 의미한다.

• 추정 값을 변경시킬 수도 있고, 안할수도 있다.

Bellman-Ford 알고리즘

• 방향 그래프, 음의 가중치를 갖는 그래프에서 SSP를 찾는 것이 목적
• 하지만 간선이 음의 가중치를 갖는 경우, 그리고 그 간선이 순환구조를 띄는 경우 최단 경로를 구할 수 없다.

• v2 → v3의 가중치 2보다 v3 -> v2의 가중치 -4가 절대값이 더 크므로,

이 순환구조로 d[v2], d[v3] = oo 가 되고, d[v4]도 oo 가 되어 결국 v1→v4의 최단경로를 구할 수 없게 된다.

• 벨만 포드 알고리즘은 SSP를 구할 수 있음은 물론, 위와 같이 최단경로에 도달할 수 없음을 false를 반환함으로써 표현할 수 있다.

• 벨만 포드 알고리즘은 정점의 개수만큼 모든 간선을 Relax하는 작업을 수행(시간복잡도 높음)
• 시간복잡도가 높음에도 벨만 포드 알고리즘을 사용하는 이유: 정확성
  • 음의 가중치가 있는 그래프의 단일 출발지 최단경로를 구할 수 있고, 그래프가 음의 순환구조를 갖는다면 이를 식별할 수 있다.

🔻

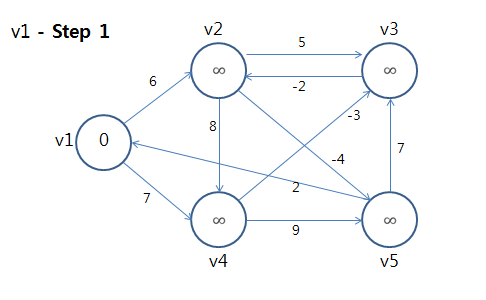
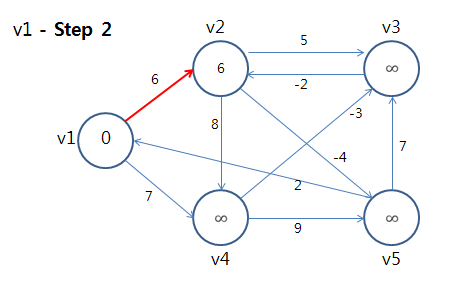
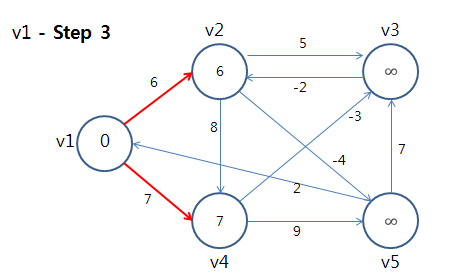
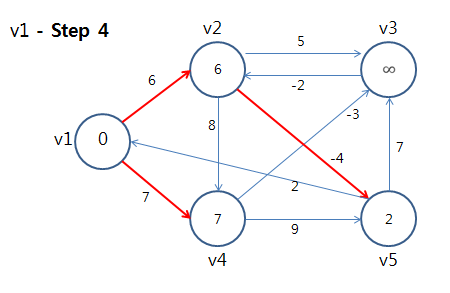
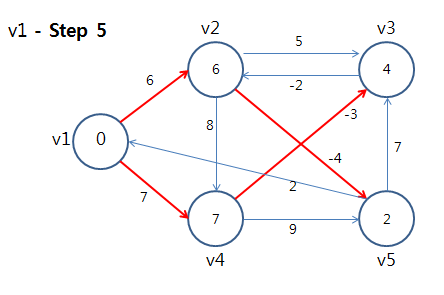
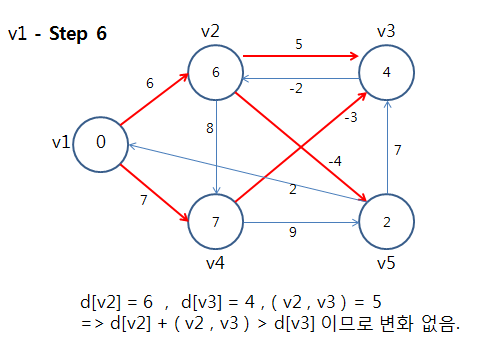
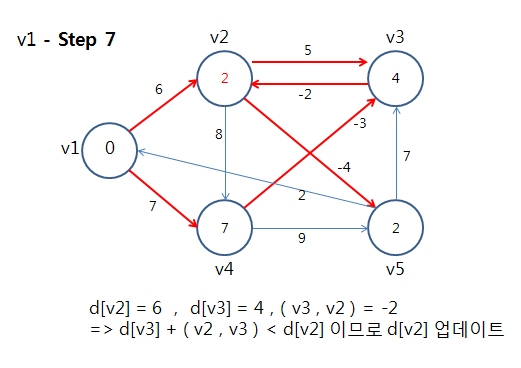
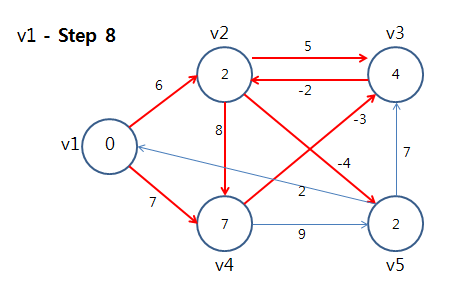
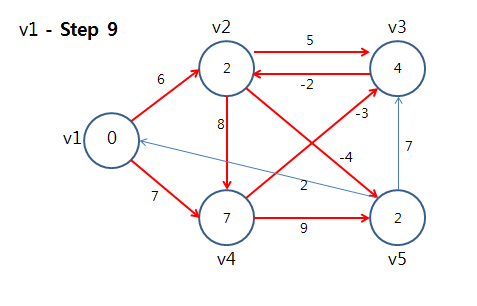
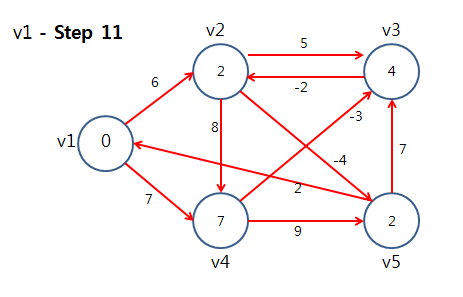
⇒ 정점 v1에 대해 모든 간선을 Relax를 했음. 이제 다음 정점을 선택하여 또 모든 간선을 Relax를 수행한다.

• Bellman-Ford 알고리즘은 정점의 개수만큼 모든 간선을 Relax하기 때문에 엄청난 연산이 수행됨
• 같은 SSP 알고리즘인 Dijkstra’s 알고리즘은 음의 가중치를 갖는 간선에 대해 SSP를 구할 수 없다.
• 시간복잡도
  • 초기화 작업 : Θ(V)

  • 음의 순환구조를 검사하는 반복문 : Θ(

    E

    )

  • 따라서 Θ(VE)

Dykstra’s 알고리즘

• 최소 우선순위 큐를 이용해서 하나의 정점으로부터 인접한 간선들을 확장해 나가는 방식
• Dijkstra’s 알고리즘은 먼저 모든 정점들을 최소 우선순위 큐에 삽입한다.
• 그리고 최단 경로 가중치 값( d[v] )이 가장 작은 정점을 선택하여 인접 간선들에 대해 Relax를 수행하여,

시작 정점으로부터 각 정점까지의 최단 경로 비용을 계산합니다.

🔻

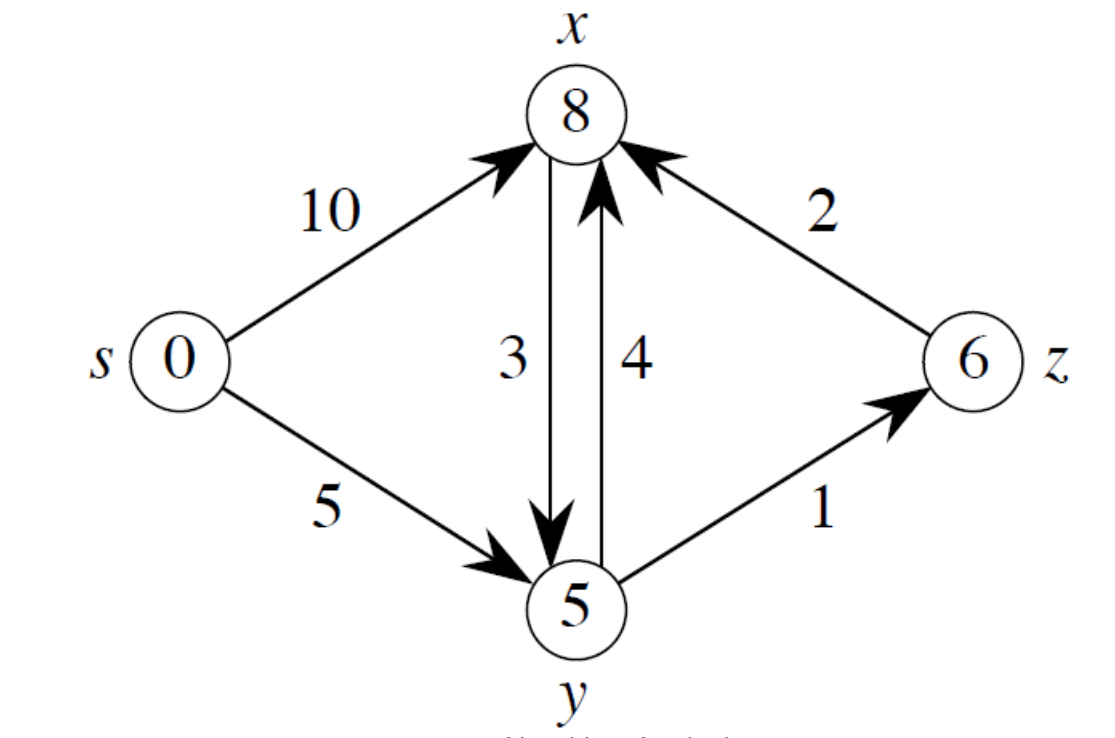
1. 모든 정점들을 최소우선순위큐에 삽입한다.

2. 최단 경로 가중치 값 ( d[v] )이 가장 작은 정점을 선택해 인접간선들에 대해 Relax를 수행하여,

시작 정점으로부터 각 정점까지의 최단경로비용을 계산한다.

Dijkstra’s Algorithm Example

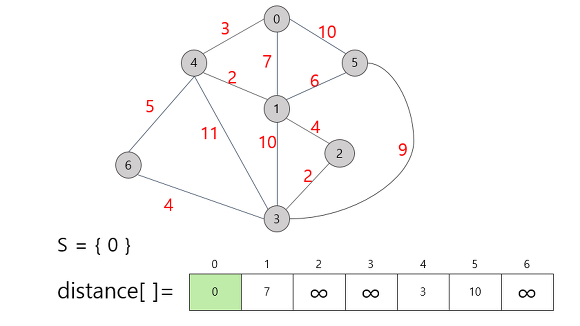
시작 정점을 0으로 잡고, 각 지점까지의 거리를 표시.

직접적으로 가는 경로가 없는 경우 무한대로 표시.

표시 되어 있는 거리 중 가장 짧은 거리는 정점 4까지의 거리인 3이므로 정점 4를 집합 S에 추가시켜준다.

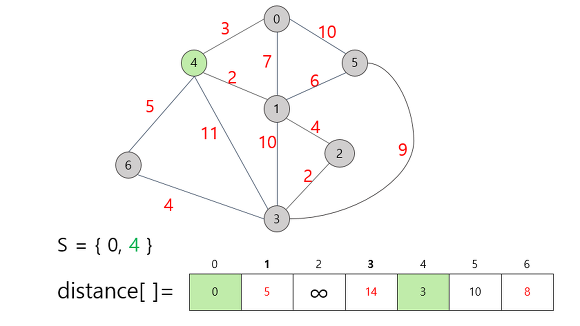
새로운 정점이 S에 추가되면 다른 정점들의 distance 값이 변경된다.

0번 정점에서는 직접적으로 갈 수 없던 정점에 새롭게 들어온 정점 4를 통해

직접적으로 갈 수 있기 때문에 무한대의 값에서 구체적인 정수거리로 정보가 갱신된다.

또한 새로운 정점 4를 통해 갈 때 더 짧은 경로가 발견 된다면 그 정보 또한 갱신을 해준다.

갱신된 정보를 바탕으로 집합 S에 추가할 다음 정점을 선택. 남은 정점 중 가중치가 가장 작은 정점1을 S에 추가하고 정보를 갱신한다.

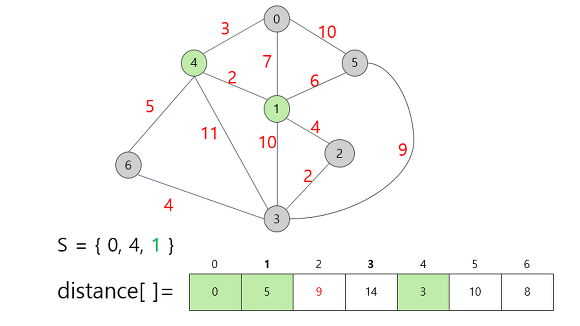
1번 정점을 추가함으로써 2번 정점까지 직접적으로 갈 수 있게 되었으므로

무한대의 값에서 구체적인 가중치인 9로 수정해준다. 현재까지의 distance 배열값을 기준으로

가장 작은 값은 6번 정점의 8이므로, 6번 정점을 택한다.

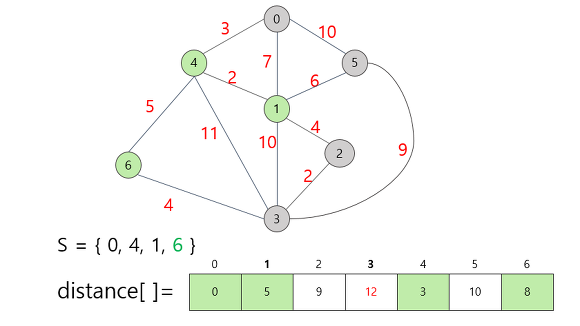
6번 정점을 집합 S에 추가함으로써 갱신할 수 있는 정보는 정점 3까지의 거리.

다음 택할 정점은 정점2

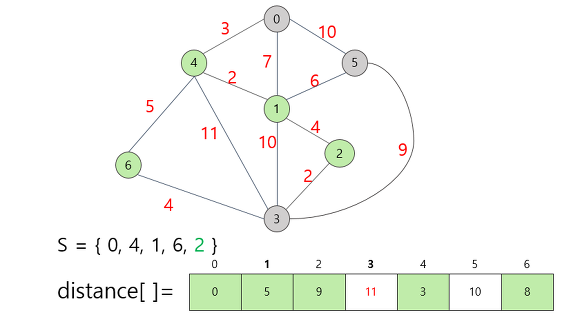
정점 2를 집합 S에 추가함으로써 정점 3까지의 거리가 갱신되었다.

가중치가 가장 적은 5번 정점을 선택하고, 갱신할 정보가 있다면 갱신한다.

그 다음은 마지막 정점인 3번 정점을 택한다.

다익스트라 알고리즘은 이러한 순서와 원리로 진행 된다.

import heapq
import sys

def dijkstra(start):
    # 초기 배열 설정
    distances = {node: sys.maxsize for node in graph}
    # 시작 노드의 거리는 0으로 설정
    distances[start] = 0
    queue = []
    # 시작 노드부터 탐색 시작 하기 위함. (거리, 노드) - 거리, 노드 순으로 넣은 이유는 heapq 모듈에 첫 번째 데이터를 기준으로 정렬을 진행하기 때문 (노드, 거리) 순으로 넣으면 최소 힙이 예상한대로 정렬되지 않음
    heapq.heappush(queue, (distances[start], start))

    # 우선 순위 큐에 데이터가 하나도 없을 때까지 반복
    while queue:
        # 가장 낮은 거리를 가진 노드와 거리를 추출
        current_distance, node = heapq.heappop(queue)
        # 파이썬 heapq에 (거리, 노드) 순으로 넣다 보니까 동일한 노드라도 큐에 저장이 된다 예시: queue[(7, 'B'), (10, 'B')]
        # 이러한 문제를 아래 조건문으로 이미 계산되어 저장한 거리와 추출된 거리와 비교하여 저장된 거리가 더 작다면 비교하지 않고 큐의 다음 데이터로 넘어간다.
        if distances[node] < current_distance:
            continue

        # 대상인 노드에서 인접한 노드와 거리를 순회
        for adjacency_node, distance in graph[node].items():
            # 현재 노드에서 인접한 노드를 지나갈 때까지의 거리를 더함
            weighted_distance = current_distance + distance
            # 배열의 저장된 거리보다 위의 가중치가 더 작으면 해당 노드의 거리 변경
            if weighted_distance < distances[adjacency_node]:
                # 배열에 저장된 거리보다 가중치가 더 작으므로 변경
                distances[adjacency_node] = weighted_distance
                # 다음 인접 거리를 계산 하기 위해 우선 순위 큐에 삽입 (노드가 동일해도 일단 다 저장함)
                heapq.heappush(queue, (weighted_distance, adjacency_node))

    return distances

graph = {
    'A': {'B': 10, 'C': 3},
    'B': {'C': 1, 'D': 2},
    'C': {'B': 4, 'D': 8, 'E': 2},
    'D': {'E': 7},
    'E': {'D': 9},
}

result = dijkstra('A')
print(result)

# {'A': 0, 'B': 7, 'C': 3, 'D': 9, 'E': 5}

#출처:https://brownbears.tistory.com/554

[출처]

https://victorydntmd.tistory.com/103

https://mattlee.tistory.com/50