DBMS는 삽입, 삭제, 스캔, 검색 기능을 필수로 제공해야 한다.

File & Index Manager의 역할은 이 기능들을 효율적으로 구현하는 것이다.

File Organization의 종류

파일구조는 레코드를 파일에 배치하는 방법을 말한다. 파일구조마다 각 연산에 따른 비용이 다르기 때문에, 주된 데이터 접근 방식에 따라 적절한 파일구조를 선택해야 한다.

비용 계산

연산의 비용 계산은 다음과 같은 변수를 사용해 표시한다.

B : File당 data block=page 개수
R : block당 record 개수
D : 디스크에서 block을 읽고 쓰는데 걸리는 평균 시간

Heap File

Untitled

가장 단순한, 순서가 없는 파일구조이다. 페이지 내의 데이터가 정렬돼있지 않다. 레코드는 유일한 rid(Record ID)를 가지며, 한 파일에 속하는 페이지는 크기가 모두 같다. (주의: 자료구조 heap과 다른 개념이다) 대부분의 데이터 접근이 풀스캔(full-scan)일 때 적절하다. 다음은 heap 파일에서 각 연산의 비용이다:

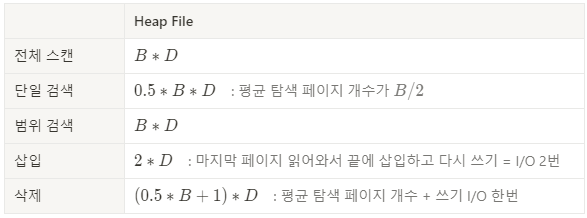
Untitled

Sorted File (packed)

Untitled

페이지 내의 데이터가 정렬되어 있는 파일구조이다. 그중 “packed”란, 삭제에 의한 공백을 허용하지 않는다는 뜻이다. 순서대로 검색 혹은 범위 검색에 적절하다. 다음은 sorted 파일에서 각 연산의 비용이다:

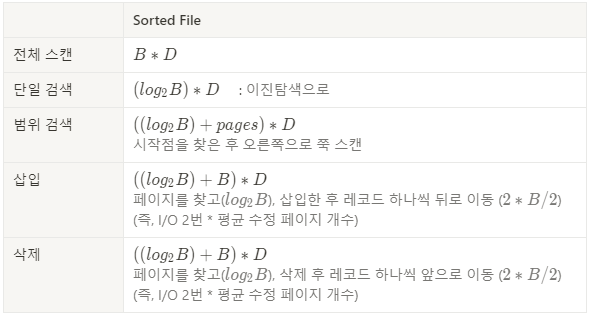
Untitled

Indexed Sequential File

순차적으로 정렬된 데이터 파일과 이 파일에 대한 포인터를 가지고 있는 인덱스로 구성된다. 인덱스를 통해 각 레코드에 접근할 수 있다. 인덱스와 순차 데이터 파일을 구성하는 방법에 따라 여러 종류로 구분되며, 그 중 ISAM과 B+트리를 살펴볼 것이다.

Index란

먼저 Index란 추가적인 저장공간을 활용해 데이터베이스 테이블에 대한 검색 속도를 향상시키기 위한 자료구조이다. 책에서 원하는 내용을 찾을 때, 모든 페이지를 찾기 보다 책의 색인을 보고 찾는 것이 훨씬 빠르다. Index는 책의 색인과 비슷한 기능을 한다. 인덱스를 타고 실제 데이터에 접근할 수 있기 때문에 Access Method라고도 한다.

테이블에서 특정 컬럼의 부분집합을 Search Key로 사용한다. 해당 컬럼에 인덱스를 생성하면, 컬럼의 데이터들을 정렬하여 별도의 메모리 공간에 데이터의 물리적 주소와 함께 저장된다. 인덱스에 실제 저장된 아이템을 Data entries라고 한다 (e.g, <key, 페이지에 대한 포인터>).

MySQL은 사용자에게 ISAM 과 B+트리, 두 종류의 index를 제공한다. 이 두 가지를 알아보자.

ISAM (Indexed Sequential Access Method)

1960년에 나온 구식 방법이지만, 정적인 데이터에 한해 최고로 효율적이기 때문에 최근까지도 사용된다. 단, 삽입/삭제에 매우 취약하며, 이 때문에 보통 B+트리를 선호한다. 정적 인덱스, 즉 트리 구조가 변경되지 않는다는 특징이 있다. 모든 변화는 leaf 노드에만 일어난다.

인덱스 생성 과정

  1. 먼저 레코드를 정렬한다.

    (순차적인 접근을 가능하게 하기 위해) 페이지는 논리적 순서에 따라 물리적으로 정렬돼있다. 따라서 각 페이지를 연결하기 위한 ‘next 포인터’는 필요 없다. (참고: 보통 빠른 삽입을 위해 페이지당 20% 정도 공간을 비워둔다)

    Untitled

  2. 그 위에 인덱스를 짓는다.

    반드시 만족해야하는 속성(“Key Invariant”)은, 왼쪽 엔트리 값보다 같거나 크고, 오른쪽 엔트리 값보다 작은 값은 항상 두 엔트리 사이에 있는 포인터를 따라가야 찾을 수 있다는 것이다. 다시 말해, 노드 엔트리가 [<Key1, Page1에 대한 포인터>, <Key2, Page2에 대한 포인터>] 일 때, Key1 이상이고 Key2 미만인 값은 항상 Page1에 있다.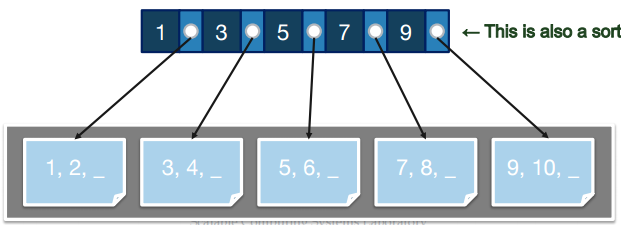

    Untitled

  3. 인덱스는 recursive하게 짓는다.

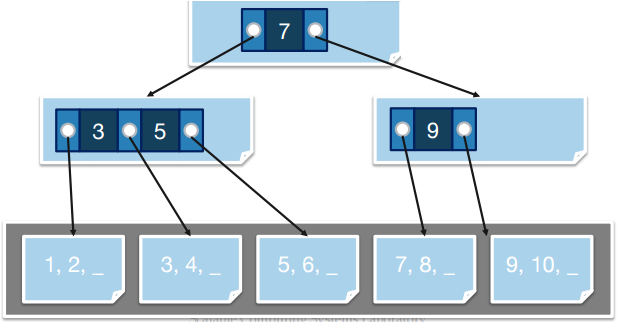
    Untitled

검색 비용

💡 검색 과정은 자료구조에서 B+트리 포스트 참고

단일 레코드를 검색하는 데 걸리는 시간은 O(logFB) (B=페이지 개수, F=fan-out)로, 다른 자료구조와 비교해 빠름을 알 수 있다.

ISAM의 단점

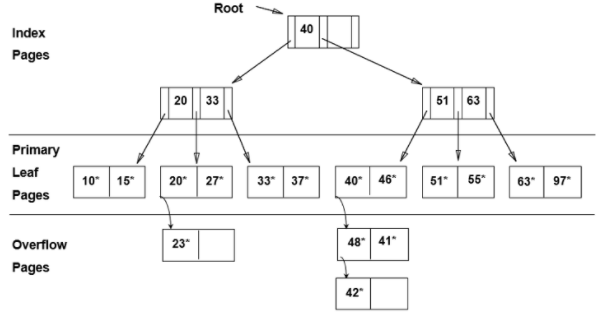
삽입/삭제에 취약하다. 이는 오버플로(overflow) 페이지 때문이다. ISAM은 삽입할 데이터가 기존 페이지에 더이상 담기지 않을 때, 파일 끝에 새로운 페이지를 추가해 새로운 데이터를 삽입한다. 문제는 이 오버플로 페이지가 기존 페이지들과 물리적으로 연속된 공간에 위치하지 않는다는 데 있다. 즉, Spatial locality가 어겨져 딜레이가 생긴다.

예를 들어, 페이지1 에 [1,2,4]가 저장돼있고 새로운 데이터 3을 넣는 상황을 가정해보자. 이때 페이지1에 더이상 공간이 없다면, ISAM은 파일 끝에 새로운 페이지n을 생성해 3을 삽입한다. 이후 순차적인 탐색이 있을 때, 1,2를 읽기 위해 페이지1을 읽어들였다가, 3을 읽기 위해 페이지n을 읽고, 이후 4를 읽기 위해 다시 페이지1을 읽어들이는 비효율적인 과정을 거치게 된다. 따라서 오버플로 페이지가 많이 생긴 경우, MySQL은 전체 DB를 다시 구축하는 것을 추천한다.

이것이 ISAM 대신 B+트리를 사용하는 가장 큰 이유이다. 단, 그래도 유지 비용이 B+트리보다 좋기 때문에, 삽입/삭제가 별로 없다면 만들기 쉽고 성능을 보장하는 ISAM도 좋은 선택지이다.

Untitled

정리하자면…

단일키 탐색 👍
스캔 👍
범위 탐색 👍
삽입/삭제 😥

B+Tree (Balanced Tree)

B+트리는 ISAM과 노드 구조나 검색 순서는 동일하다. 하지만 정적 인덱스인 ISAM과 달리, 동적 인덱스이다. 레코드가 늘어남에 따라 페이지가 동적으로 할당되며, 따라서 실제 물리적인 데이터 페이지가 논리적 순서를 따라 저장돼있지 않다. 그렇기 때문에 페이지간 쉬운 순회가 가능하도록 next, prev 포인터가 필요하다. 또한, 항상 balanced 상태를 유지해야하기 때문에 삽입/삭제 모두 꽤 시간이 걸린다. 결국, B+트리는 ISAM의 단점을 없앤 대신, 거의 모든 작업에서 최선의 성능을 내진 못한다.

B-트리는 BST(Binary Search Tree)를 확장한 자료구조이고, B+트리는 B-트리를 개량한 자료구조이다. B-와의 가장 큰 차이점은 Inner Node에는 Key만 저장이 되고 Leaf Node에 Key와 Data를 함께 저장한다는 점이다. Leaf Node에만 Data가 저장되기 때문에 Leaf Node 사이를 포인터로 연결하여 쉬운 순회가 가능하도록 만든점도 B+ Tree의 특징이다.

💡 검색, 삽입, 삭제 과정은 자료구조에서 B+트리 포스트 참고
혹은 다음 애니메이션 참고: Great animation online of B+ Trees

정리하자면…

단일키 탐색 👍
스캔 🤷
범위 탐색 🤷
삽입/삭제 👍

-> 스캔과 범위 탐색에서 성능이 보장되지 않는 것은 leaf 노드 페이지가 순차적으로 저장돼있지 않을 수도 있기 때문이다. 이 문제는 벌크 로딩을 사용해 해결할 수 있다!

Bulk Loading B+ Tree

큰 테이블에 대한 인덱스를 새로 짓는 상황을 가정해보자. 한 가지 방법은 빈 트리에 레코드를 일일이 삽입하는 것이다. 이 방법은, 특히 레코드가 랜덤한 순서로 있다면, 매우 비효율적이다. 이에 대한 대안책으로 벌크 로딩(Bulk Loading)을 사용한다.

  1. 레코드를 search key에 대해 정렬한다.

  2. Leaf 노드를 그 부모 노드가 가득 찰 때까지 채운다.

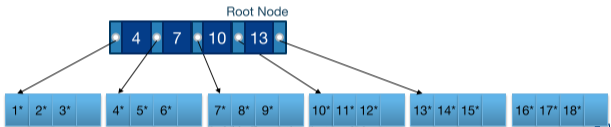
    Untitled

  3. 부모 노드를 나눈다.

    Untitled

벌크 로딩을 사용해 지은 B+ 인덱스의 장점

  • 훨씬 적은 I/O로 인덱스를 지을 수 있다.
  • 페이지의 fill factor를 통제할 수 있다. 즉, 각 페이지를 어느 정도까지 채울 것인지 컨트롤 가능하다.
  • Leaf 노드 페이지가 물리적으로 연속된 공간에 위치할 것이다.

정리하자면…

단일키 탐색 👍
스캔 👍
범위 탐색 👍
삽입/삭제 👍


참고자료
  • https://wkdtjsgur100.github.io/db-summary/
  • https://middleware.tistory.com/entry/%EB%8D%B0%EC%9D%B4%ED%84%B0-%EA%B5%AC%EC%A1%B0-%EB%B0%8F-%ED%8C%8C%EC%9D%BC-%EA%B5%AC%EC%A1%B0
  • https://mangkyu.tistory.com/96
  • https://coding-factory.tistory.com/746
  • https://untitledtblog.tistory.com/79